Computers: The OR operator

By -

The OR operator

The second logical operator is OR. Using the party example from the previous sections,

image

The electrical circuit shown in Figure 2.4 reproduces the effect of this table. In this circuit, the switches A and B are in parallel, and current X will flow if either A orB (or both) are closed.

image

clip_image006

The NOT operator

The third logical operator is NOT. In the example we have used already, NOT A means Ann is not going (to the party)

and NOT B means Barbara is not going. So if Ann is going is true, then NOT A is false. The truth table representing this is:

image

In electronics, a NOT gate consists of a special sort of switch which closes and so makes a circuit when no current is applied to it, and opens and so breaks the circuit when there is a current.

clip_image007

Combining logical operators

We can combine these logical operators (and the circuits which represent them) in any number of ways. Staying with the party example, Colin may decide to go to the party if:

(A OR B) AND NOT (A AND B) = 1

This means he will go to the party if

A ORB= 1, i.e. if Ann or Barbara go, AND if NOT (A AND B) = 1, i.e. if they don't both go.

So he'll go with one or the other but not both.

The truth table for this can be built up in stages. The first stage is to construct intermediate values for A OR B and NOT (A AND B). The stage combines these two intermediate results using the AND operator.

image

Arithmetic and logic

Most of the work done by a computer involves arithmetic calculations. The basic task in this arithmetic is the addition of the two binary numbers 0 and 1. If A and B can each take either of these two values, the resulting values of A + B will be as follows:

image

The last column of this table, which shows the results of the addition, really consists of two columns: a two's column (i.e. 10 in binary) and a units column. So we could rewrite the table like this:

image

Notice that the two's column is identical to the results column of the A AND B truth table on page 26. The units column is the same as the results column of the (A OR B) AND NOT (A AND B) table in the last section.

This means that we can use logical operators, and there­ fore logic gates, to produce these two columns, and there­ fore to carry out binary calculations.

clip_image009Logic circuits

Logic gates, shown as the simple electrical circuits on earlier pages in this chapter, therefore lie at the heart of all computing. As you have learned, these gates consist of switches connected up in various ways. In a microprocessor,

image

each switch is a transistor, and a gate is therefore a simple circuit containing two or more transistors.

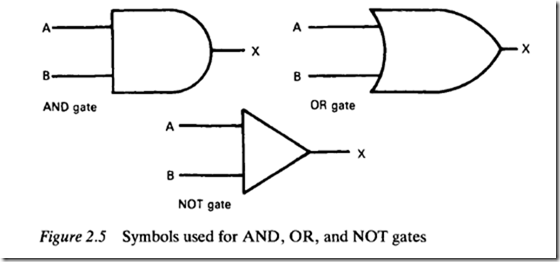
Rather than draw these circuits each time we wish to show an AND, OR, or NOT gate, it is much easier to use symbols. These are shown in Figure 2.5. Figure 2.6 shows a circuit called a 'half-adder gate' which produces the (A OR B) AND NOT (A AND B) column of the above truth table.

(If you study this circuit, you will see that it does indeed represent this combination of logical operators.) As you learned in the last section, it is this combination of gates that carries out the basic task of addition.

There are other kinds of circuits used in the arithmetic logic units of computers, but they are all based upon the logical operators described in the previous sections, and consist of various combinations of the AND, OR, and NOT gates.

image

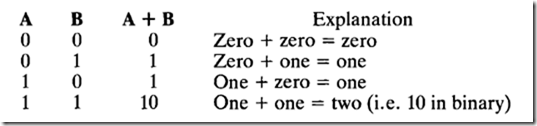
Comments

Post a Comment

Popular posts from this blog

The Conversion Cycle:The Traditional Manufacturing Environment

By -
Image
The Traditional Manufacturing Environment The conversion cycle consists of both physical and information activities related to manufacturing products for sale. The context-level data flow diagram (DFD) in Figure 7-1 illustrates the central role of the conversion cycle and its interactions with other business cycles. Production is triggered by customer orders from the revenue cycle and/or by sales forecasts from marketing. These inputs are used to set a production target and prepare a production plan, which drives production activities. Purchase requisitions for the raw materials needed to meet production objectives are sent to the purchases procedures (expenditure cycle), which prepares purchase orders for vendors. Labor used in production is transmitted to the payroll system (expenditure cycle) for payroll processing. Manufacturing costs associated with intermediate work-in-process and finished goods (FG) are sent to the general ledger (GL) and financial reporting system. Dependin...
Read more

The Revenue Cycle:Manual Systems

By -
Image
Manual Systems The purpose of this section is to support the system concepts presented in the previous section with models depicting people, organizational units, and physical documents and files. This section should help you envision the segregation of duties and independent verifications, which are essential to effective internal control regardless of the technology in place. In addition, we highlight inefficiencies intrinsic to manual systems, which gave rise to modern systems using improved technologies. SALES ORDER PROCESSING The system flowchart in Figure 4-12 shows the procedures and the documents typical to a manual sales order system. In manual systems, maintaining physical files of source documents is critical to the audit trail. As we walk through the flowchart, notice that in each department, after completion of the assigned task, one or more documents are filed as evidence that the task was completed. Sales Department The sales process begins with a customer cont...
Read more

Nassi-Shneiderman charts

By -
Image
Nassi-Shneiderman charts 56.1 Purpose Nassi-Shneiderman charts were developed by Nassi and Shneiderman as an alternative to traditional logic flowcharts. Their intent was to provide a structured, hierarchical, graphical view of the flow of logic through a program, a routine, a module, or a process. Nassi-Shneiderman charts are used to document, plan, and design detailed program logic. 56.2 Strengths, weaknesses, and limitations A properly prepared Nassi-Shneiderman chart can illustrate the flow of logic through a module or routine at a glance. Nassi-Shneiderman charts are useful for describing or planning relatively small modules, routines, or processes. They can be used to clearly show nesting and recursion, and are easily converted to structured code. Nassi-Shneiderman charts should not be used for documenting complete programs or large routines. As a general rule, Nassi-Shneiderman charts should be limited to a single page with no more than 20 subdivisions. For larger rout...
Read more