Computers: How a microprocessor handles information.

How a microprocessor handles information

The old-fashioned thermionic valve and the modern transis­tor are said to be bistable, because they can be in only one of two states, in this case either ON or OFF. Other devices used in computers and IT equipment are also bistable. For example:

• A spot on the surface of storage devices such as magnetic disks or tapes can be either magnetized or demag­netized.

• A hole position on paper tape can be either punched or not punched.

• A spot on the surface of a compact disc can either have a pit burnt in it or not.

This means that microchips and other IT devices store information as sequences of ON/OFF switches, or sequences of magnetized/demagnetized spots, or sequences of holes/ no-holes. If we call an ON switch (or a magnetized spot, or a hole) 1, and an OFF switch (or demagnetized spot, or no­ hole) 0, then all information must be broken down into sequences of 1s and Os to be handled by a computer or other microprocessor-based equipment.

For example, when you type the letter A on a computer keyboard, it is converted to the following sequence of eight 1s and 0s:

01000001

The letter B is converted to 01000010, the letter C to 01000011, the letter D to 01000100, and so on.

To reach the CPU, a 1 becomes a strong pulse of electricity travelling down the wire linking the keyboard to the rest of the computer, and a 0 becomes a weak pulse. When they reach the CPU, each weak pulse switches a transistor OFF, while a strong pulse turns a transistor ON. In this way a letter pressed on the keyboard is converted to an ON/OFF switch sequence inside the computer.

Pocket calculators work in a similar way, as does every other microprocessor-based device. When you use drawing software to draw a picture on the computer screen, the computer converts your artistry into sequences of 0s and 1s which give screen coordinates, colours, and other infor­mation about each point of your picture. If you speak into a speech recognition device (see Chapter 3), your words are converted to sequences of 0s and 1s.

These Os and 1s are, of course, numerical digits, which is why computers and other IT devices are said to be digital. In the past, some computers were not digital, but instead represented data as varying voltages. These were called analogue. I compared digital and analogue devices in Chap­ ter 1 on page 10. Modern microprocessors are so cheap and powerful that almost all IT devices are now digital.

2.5 Binary numbers

Each of the sequences of 0s and 1s described in the last section is an item of numerical data. Back at school, you probably met numbers that use just the two digits 0 and 1: they are called binary numbers. They relate to ordinary decimal numbers as follows:

and so on. Can you discern the pattern in this?

The digits 0 and 1 that make up a binary number are called binary digits, or bits for short. In most computers, information is handled in groups of eight bits, which is why there are eight 0s and 1s in the binary representations of A, B, C, and D above. A group of eight bits is called a byte, which may be short for 'by eight'.

As I said earlier, microprocessors contain many thousands of transistors, and magnetic disks and other IT equipment also contain huge numbers of bistable devices. To cope with quantities of this magnitude we use the following terms:

• Kb or Kbyte (short for kilobyte), meaning about 1,000 bytes (1024, to be exact).

• Mb or Mbyte (short for megabyte), meaning about 1,000,000 bytes (1024 Kb, to be exact).

• Gb or Gbyte (short for gigabyte), meaning 1,000,000,000 bytes (1024Mb, to be exact).

Microprocessors and logic

(The next sections are slightly more technical than other parts of the book. If you wish, you can omit them and turn straight to the section 'Microprocessors and computers' on page 32.)

Computers operate according to the rules of logic. That's why the heart of the CPU is called the 'arithmetic logic unit' (ALU). To this end, the glass valves in the earliest com­ puters, and the transistors in modern microprocessors, are organized into what are called logic gates. These enable the microprocessor to perform the logical operations AND, OR, and NOT. The significance of this is that by combining these operations, the microprocessor can carry out arithme­ tic computations on the information that is fed into it.

So to explain how microprocessors compute, we need to look into the rules governing logical operators. They come from Boolean algebra, a branch of mathematics developed by Boole in the first part of the last century. These rules go something like this.

Any proposition can be true or false. For example, the proposition Ann is going to the party is either true or false, as is the proposition Barbara is going to the party. We'll call the first proposition A and the second B. We'll also use the number 1 to represent true and the number 0 to represent false. So in the language of Boolean algebra,

A = 1 means: Ann is going to the party is true

A = 0 means: Ann is going to the party is false.

Similary,

B = 1 means: Barbara is going to the party is true

B = 0 means: Barbara is going to the party is false.

The AND operator

We can combine the propositions like those in the above example using the logical operators, AND, OR, and NOT. For example,

We can represent statements like this by a truth table. A truth table for this example shows the effect of different values of A and B on the values taken by A AND B:

The first line of this table means:

If Ann is going is false, and if Barbara is going is false, then Ann and Barbara are going is false.

The AND gate

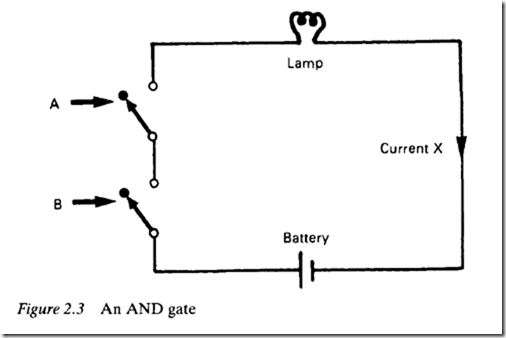
Figure 2.3 shows a simple electrical circuit which per­ forms the AND operations described above. It is called an AND gate. The switches at A and B in this circuit are mechanical devices called solenoids, and the lamp in the circuit is ON when a current flows, and OFF when it does not flow. (In a microchip, each switch in an AND gate is a transistor).

An electrical current in wire A closes the switch at A, and an electrical current in wire B closes the switch at B. In order to complete the circuit and allow the current marked X to flow from the battery to the lamp, both switches have to be closed, i.e. there has to be a current in wire A and in wire B. If either one of these wires has no current flowing in it, then one of the switches will be open and no current will flow through the lamp.

Using 1to represent the flow of current and 0 to represent the absence of current, we can draw up a truth table showing the values of X for different values of A and B. If you try this, you will see that the truth table is identical to that produced in the last section for the AND operator, and proves that this circuit correctly represents the action of that operator.